3. Angular Acceleration

$$\alpha = \dfrac{\Delta \omega}{\Delta t}$$

 

$$\lim_{\Delta t \to 0} \dfrac{\Delta \omega}{\Delta t} = \dfrac{d\omega}{dt}$$

Acceleration

A vector quantity that describes how the angular velocity of an object changes with time

For an object moving in a circle, acceleration can be decomposed into two components

• Tangential Acceleration — changes the magnitude of the angular velocity
• Radial (Centripetal) Acceleration — points toward the centre of the circular path and changes the direction of the velocity

$$\vec{a} = \begin{pmatrix} a_t \\ a_c \end{pmatrix}$$

Deriving $a_t$ and $a_c$

$$v = \omega r$$

take the derivative with respect to time

$$\dfrac{dv}{dt} = \dfrac{d\omega}{dr}r + \omega\dfrac{dr}{dt}$$

this can be rewritten as

$$a = \alpha r + \omega\dfrac{dr}{dt}$$

Angular Acceleration ($a_c$)

$$a_c = \alpha r$$

Tangential Acceleration (a_t)

$$a_t = \omega\dfrac{dr}{dt}$$

 

Contants Angular Acceleration

$$\alpha = \text{constant} \\ \; \\ d\omega = \alpha dt$$

integrate both sides

$$\int_{\omega_0}^{\omega} d\omega = \int_{0}^{t} \alpha \, dt$$ $$\; \\ \omega - \omega_0 = \alpha t$$ $$\boxed{\omega = \omega_0 + \alpha t}$$

if we solve for $\theta$

$$\dfrac{d\theta}{dt} = w_0 + \alpha t$$ $$\int_{\theta_0}^{\theta} d\theta = \int_{0}^{t} (\omega_0 + \alpha t)\, dt$$ $$\theta - \theta_0 = \omega_0 t + \frac{1}{2}\alpha t^2$$ $$\boxed{\theta = \theta_0 + \omega_0 t + \frac{1}{2}\alpha t^2}$$

 

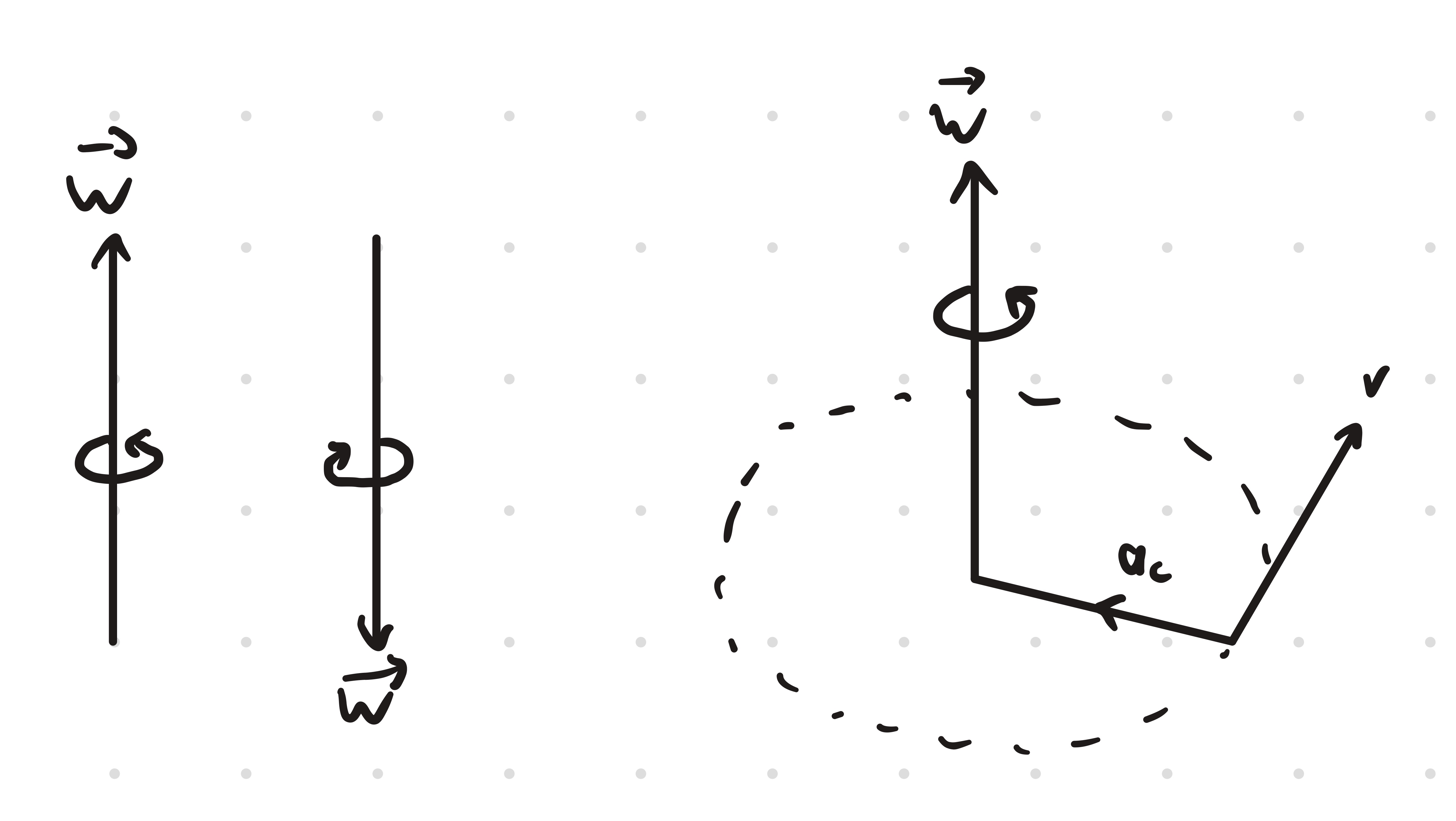
Representing $\omega$

Angular velocity can be denoted by the right hand rule